点击上方蓝字和“好玩的MATLAB”一起快乐玩耍吧!
6 J3 A2 D& f. z' a
9 c2 A' `. ]7 X
42gfzvnnwgn6408888516.jpg
 : e; H9 M" U& \4 n4 }0 ]
: e; H9 M" U& \4 n4 }0 ]
好玩的matlab5 f/ {! O, W8 h: h) I2 @" E* N. d! d
带你解锁不一样的matlab新玩法
8 Q! W4 j' {: i' `- o) g6 w1 y: J/ [; h) k( \
喜欢此推文的小伙伴们记得点赞+关注+分享!
- h& }; @( V$ f0 t) r3 x01& u+ q n+ x/ H
算法用途
! Y% m7 h1 } [+ h; K
% l* j8 Z0 m4 d" ~0 ^: Y
mhdiuedngmy6408888616.png

0 T/ ~1 ^) ^, a5 m( U3 w3 z& |: f1 S" Y优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值。
# n ]6 V5 a3 x* w' {现实问题中,很多都需要用到优化。可以说优化随处可见。在普通的函数寻找极值、空间配置、背包问题、旅行商问题中都需要用到优化算法。在机器学习中优化算法能够帮助我们在大量的迭代中快速训练模型。" E& S5 X; T/ p1 l4 G& D( {; r0 n
4 a7 F* m1 s6 y0 t
02
& r0 H9 x1 @$ w/ v" F实例分析
$ p& p) u9 w9 |% K- ` t6 @+ {" B# H# k$ K6 Z7 }; e! B7 ~% i6 h
上一篇介绍背包问题的优化。在书:MATLAB智能优化算法:从写代码到算法思想【1】中的第二章提到了用智能算法求解旅行商问题。为了对照结果,此篇选用文中的数据,并与结果进行对照。& n! ~0 Y N) t" B/ x, u1 E6 K
现有52个城市的二维坐标点如下,每个城市去一次,规划最短路线。" t: l7 m k: ~" Y" r) n
ukvrnqcss0l6408888716.png
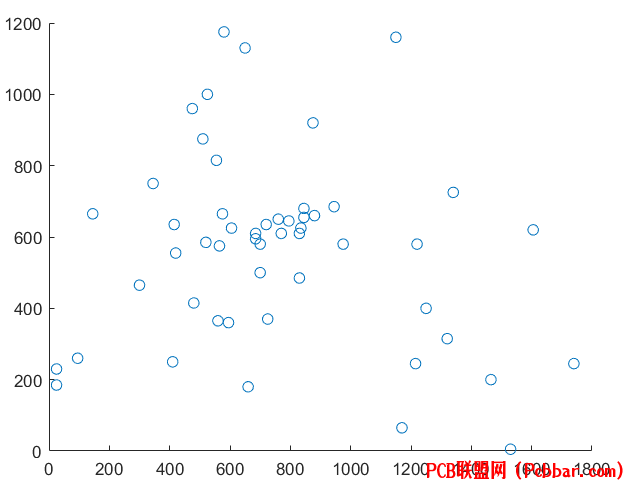 8 L! ?6 W' G A. C0 L6 q
8 L! ?6 W' G A. C0 L6 q
" A8 O% r! c* Q# L
最后书中的求解结果如下,此篇用MATLAB和python求解与以下结果对照。, k4 q" R! Y* v: J
actuwxrzjec6408888816.jpg
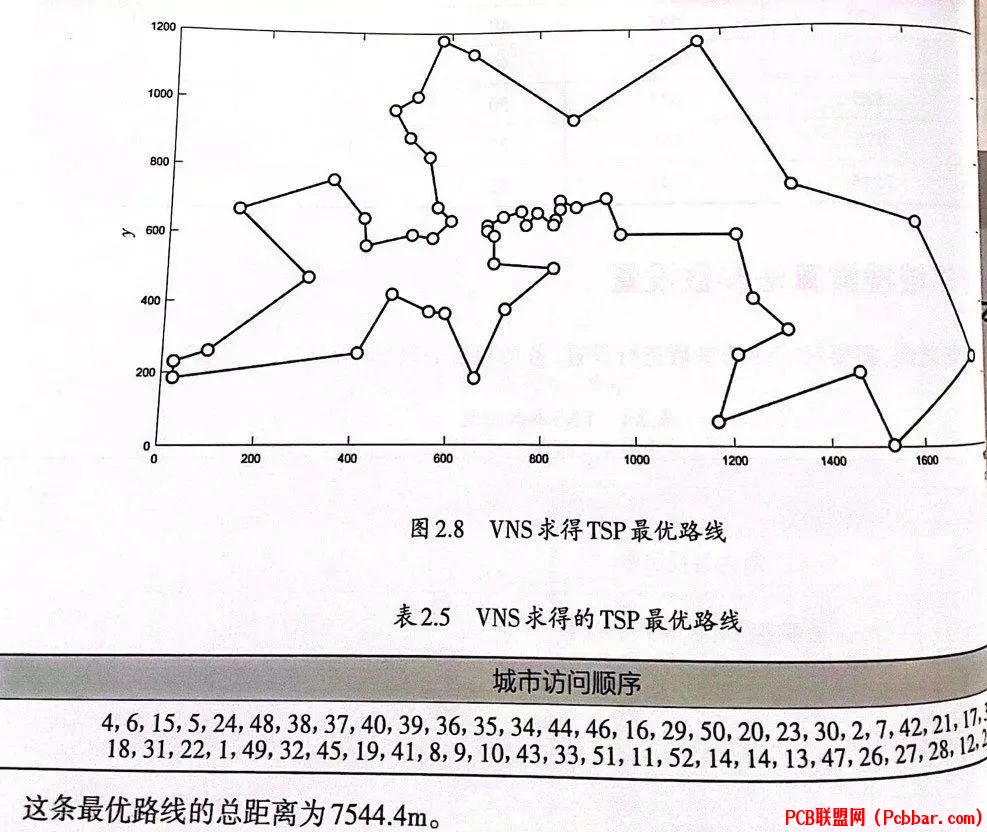
, v ]! S5 G$ |8 G% C h3 Z$ P! T2 j3 E) R
03* {+ T7 L/ h ?9 v& [: w
模型建立- B2 }+ d4 t/ _! v0 u
3 J6 c! o, |+ J
此篇模型建立和求解参考链接【2】。
2 ~3 o& G3 A. z! G: I假设 为第 个城市与第 个城市之间的距离(注意将对角线数设成一个比较大的数,对角线本来应该是0), 为城市数, 为第 个城市与第 个城市之间的决策变量,此为0-1变量,0代表第 个城市与第 个城市之间不相连、1代表第 个城市与第 个城市之间相连。我们要建立的目标即为经过所有城市距离最短,我们的约束条件即为每个城市只经过一次。所以可以建立模型如下:" {3 Z% J' y, o$ o6 i9 a. a" A
9 s, j/ Y% m4 h2 I. W, w# X$ o2 _
' b' C% U7 R7 F+ J6 |9 v% z
3 m& M3 ?$ V5 Y) \; M3 @( e( z 为0或1, 为实数。需要注意的点为此建模将距离矩阵 的对角线的0全部替换成比较大的数,以防总是在同一个城市徘徊。约束条件前两个就是保证每个城市只去一次,最后一个约束条件即为防止子回路的出现,下面会介绍子回路出现的情况。
1 w% b* S6 N) T( n, O; i B
. x+ q# C9 e- z# h/ |# V/ N1 a7 \: v. }) j8 n2 L" Z
2 _# j1 w- w: m# t5 M046 l' n( E i* K" h
MATLAB求解
- u, c" v8 b2 o9 A' [% O
# c% h0 Q8 j2 B6 M0 ~yalmip求解- O( ?4 r- U6 ~ E S# c
' y) b( X5 @# b6 | W! T9 ]/ l2 r* `
4 I9 \8 ]! _. C& d' B1 N4 _0 V2 u9 B8 y定义变量,计算距离矩阵
9 g8 K6 p- Y3 O- _6 o, N& a6 Q) m+ V" N3 T
在这个问题中, 为52*52的矩阵0-1变量, 为52*1的实数变量。
6 X4 X, K3 [3 b" tsdpvar实型变量,intvar 整型变量 binvar 0-1型变量
: T7 I9 a/ f4 z7 e# r# f/ c对于此问题的变量可以定义为:
" m2 Y% y# G+ a1 Q/ c" _$ ], x%点坐标data_x=[565;25;345;945;845;880;25;525;580;650;1605;1220;1465;1530;845;725;... 145;415;510;560;300;520;480;835;975;1215;1320;1250;660;410;420;575;1150;700;... 685;685;770;795;720;760;475;95;875;700;555;830;1170;830;605;595;1340;1740];%y点坐标data_y=[575;185;750;685;655;660;230;1000;1175;1130;620;580;200;5;680;370;665;... 635;875;365;465;585;415;625;580;245;315;400;180;250;555;665;1160;580;595;... 610;610;645;635;650;960;260;920;500;815;485;65;610;625;360;725;245]; %% 计算各个坐标点之间的距离num=length(data_x); %城市点的个数distance_juzheng=zeros(num,num);for i =1:num for j=1:num if (i ~=j) distance_juzheng(i,j)=sqrt((data_x(i)-data_x(j))^2+(data_y(i)-data_y(j))^2); else distance_juzheng(i,j)=100000; end endend%%%定义变量,x为0-1变量记录,表示x=binvar(num,num,'full');u=sdpvar(1,num);在此对角线的0被换成了100000,定义 x=binvar(num,num,'full') ,默认矩阵变量是对称的所以加一个'full',即可满足定义
* m! T* ?- R( T/ [9 _0 L% t
5 d @% c* F/ q: D! o+ {4 x3 y+ Q目标函数
( @% ^$ u& K5 @8 ]9 X& U6 I$ D. D+ p Q. L
G* C4 }, r- |! q1 w, R) T( z
0 C5 k8 v' z: D
( z. ^' M$ ~& N l7 O: _
! s! \3 [* x9 z: }%目标函数obj=sum(sum(x.*distance_juzheng));. P4 m! j$ \2 q% j- P
约束条件" k/ O& l. \; A6 I- J" T
; s( ?5 g; g4 I' e* G5 f0 B' P/ r; u; \9 h0 n( [4 n
6 ?3 A4 s8 ^7 W7 Z- G; F0 }( ~0 j8 B
+ D' A! I, X3 {& @
, D/ Z2 A3 O: U# ^/ S
; S9 l! w: K7 S, S $ {9 k* q( H6 ^% n$ R0 ^" w+ {
. ]* d% k* k& }
%约束条件%1.每个城市只能经过一次 ,0-1矩阵每一行加起来只能为1,每一列加起来只能为1.constr=[]; %循环添加约束条件for i = 1:num constr = [constr, sum(x(i,:)) == 1];endfor j = 1:num constr = [constr, sum(x(:,j)) == 1];end% 约束条件2,不允许出现子回路for i = 2:num for j = 2:num if i~=j constr = [constr,u(i)-u(j) + num*x(i,j)num-1]; end endend: [2 J7 m+ a3 |% a' S5 c7 t" D9 p7 e
优化求解
" L h9 X4 N7 }5 {8 ?+ qoptimize(constr,obj)$ n, d( v5 R- p. M
完整代码
/ @; w* P9 ]" Q5 i! }" uclc;clear;close all;%点坐标data_x=[565;25;345;945;845;880;25;525;580;650;1605;1220;1465;1530;845;725;... 145;415;510;560;300;520;480;835;975;1215;1320;1250;660;410;420;575;1150;700;... 685;685;770;795;720;760;475;95;875;700;555;830;1170;830;605;595;1340;1740];%y点坐标data_y=[575;185;750;685;655;660;230;1000;1175;1130;620;580;200;5;680;370;665;... 635;875;365;465;585;415;625;580;245;315;400;180;250;555;665;1160;580;595;... 610;610;645;635;650;960;260;920;500;815;485;65;610;625;360;725;245];%% 显示一下坐标点figure(1)scatter(data_x,data_y,40)%% 计算各个坐标点之间的距离num=length(data_x); %城市点的个数distance_juzheng=zeros(num,num);for i =1:num for j=1:num if (i ~=j) distance_juzheng(i,j)=sqrt((data_x(i)-data_x(j))^2+(data_y(i)-data_y(j))^2); else distance_juzheng(i,j)=100000; end endend%%%定义变量,x为0-1变量记录,表示x=binvar(num,num,'full');u=sdpvar(1,num);
" l. X7 K0 x8 H8 P, v E$ H7 ]/ N/ O%目标obj=sum(sum(x.*distance_juzheng));
6 m1 D/ x3 e. _) @/ D. V. w%约束条件%1.每个城市只能经过一次 ,0-1矩阵每一行加起来只能为1,每一列加起来只能为1.constr=[]; %循环添加约束条件for i = 1:num constr = [constr, sum(x(i,:)) == 1];endfor j = 1:num constr = [constr, sum(x(:,j)) == 1];end% 约束条件2,不允许出现子回路for i = 2:num for j = 2:num if i~=j constr = [constr,u(i)-u(j) + num*x(i,j)1]; end endend%优化%%optimize(constr,obj)disp('自变量矩阵为')disp(value(x))" H, ~7 m, R1 F* X8 r- V, M
disp('目标函数最优值')disp(value(obj))9 b+ b# F5 q. h# s2 x
%% 画图展示bianlian=value(x);index_all=[];for i=1:num if i==1 index=find(bianlian(:,i)==1); else index=find(bianlian(:,index_all(i-1))==1); endindex_all=[index_all,index];endindex_all=[index_all,index_all(1)];% {$ c. {* R4 z/ f$ i5 c4 I
figure(2)for n=1:numplot(data_x(index_all(n:n+1)),data_y(index_all(n:n+1)),'--o','Color',[135,206,235]./255,'MarkerSize',8,'MarkerFaceColor',[160,102,211]./255,'LineWidth',2);hold on endtitlestr=['最佳路径如下', ' 最短距离为:',num2str(value(obj))];title(titlestr)xlabel('x坐标')ylabel('y坐标')
/ U, J8 R7 |. l) u' l
R3 V9 u1 j( M, L3 y, V
wcfdrytlhvz6408888916.png
 5 A9 ?6 W. v7 I6 Q" E0 ^; _
5 A9 ?6 W. v7 I6 Q" E0 ^; _
和书中求解结果一致; W7 w9 V8 d! ^( ^
5 H6 [4 J1 x/ [$ y6 j8 q
如果缺少最后一个约束,即防止子回路的约束,就会出现以下情况,一直在第一座城市和第二座城市之间徘徊,一共经过2个城市。
- K0 n% g6 ^) ?0 ^, D' K
rbuk0aa2nk46408889017.jpg
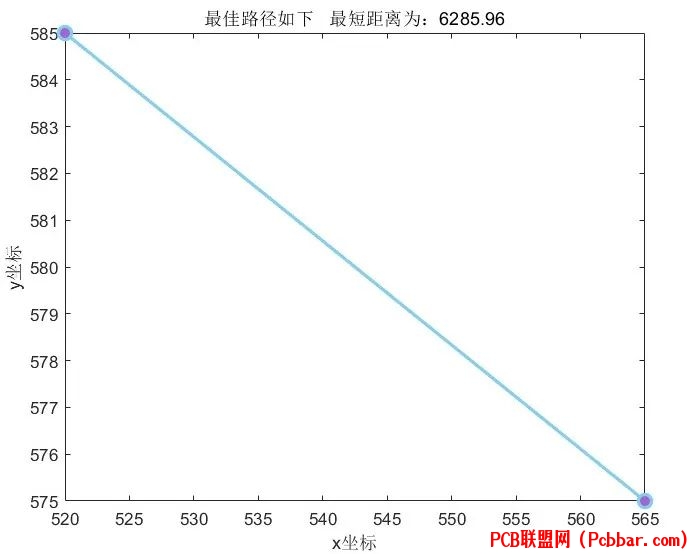
* |3 d% X* f! z" I' P* u1 ]: r% M9 e
04! c1 `! S8 ?7 T- X
python求解
; N0 Z6 _& @, G% h M9 ` G3 K& w, b- U/ V3 y# I* i) P+ I0 f
在python中也有一款受欢迎的优化软件gurobi,gurobi是由美国Gurobi公司开发的新一代大规模数学规划优化器。安装gurobi可以网上找教程。用gurobi求解:1 }* x, B* H% D7 Z& g! J) t
导入包( n+ {9 ~5 @0 u3 U
from gurobipy import *import numpy as np
" }2 W/ m% `; M3 E l' X; Q3 ^创建模型7 C/ S* {4 P/ h9 {
model=Model("question1")
/ u; z; i: U5 T- J5 `" m% Z! U定义变量,计算矩阵
5 S, \$ ?; X6 U0 Z* t1 ` Z% s7 Q" u
: {; T/ z, i3 d; rvtype=GRB.BINARY 二进制变量,0-1变量vtype=GRB.CONTINUOUS 连续变量vtype=GRB.INTEGER 整数变量lb 是变量下限,ub是变量上限
% z4 l( K' L. Q. `! E' _- a在这个问题中, 为52*52的矩阵0-1变量, 为52*1的实数变量。
# \; c& h& Z2 A, R- O1 Vsdpvar实型变量,intvar 整型变量 binvar 0-1型变量$ L& ?: e' o/ x8 J/ K
对于此问题的变量可以定义为:
! r8 E, N1 h% }# x点坐标data_x=[565,25,345,945,845,880,25,525,580,650,1605,1220,1465,1530,845,725, 145,415,510,560,300,520,480,835,975,1215,1320,1250,660,410,420,575,1150,700, 685,685,770,795,720,760,475,95,875,700,555,830,1170,830,605,595,1340,1740]# y点坐标data_y=[575,185,750,685,655,660,230,1000,1175,1130,620,580,200,5,680,370,665, 635,875,365,465,585,415,625,580,245,315,400,180,250,555,665,1160,580,595, 610,610,645,635,650,960,260,920,500,815,485,65,610,625,360,725,245]8 \! h' T6 @6 q6 e
data_num=len(data_x)
9 ~) y0 V" s7 G2 N6 H! D$ ldistance_juzheng=np.zeros((data_num,data_num))
# ^; z- l# \4 Z: o# d' A/ V% jfor i in range(0,data_num): for j in range(0,data_num): if (i==j): distance_juzheng[i,j]=100000 else: distance_juzheng[i,j]=np.sqrt(np.square((data_x-data_x[j]))+np.square((data_y-data_y[j])))
1 [( \6 k; j; ]#定义变量x=model.addMVar((data_num,data_num),lb=0,ub=1,vtype=GRB.BINARY) #lb变量下限, ub变量上限 u=model.addMVar((data_num),vtype=GRB.CONTINUOUS) #lb变量下限, ub变量上限
$ c' f6 p( q5 S2 b$ X4 S* d( O目标函数1 e9 }! G/ l5 t' \% f
3 k( `6 i2 s4 O) `5 I
7 g# \! ^7 ^# h$ P
) |& `3 G+ U; I# M$ C/ t" D
#构造目标函数objsum=[]for i in range(0,data_num): for j in range(0,data_num): objsum=objsum+x[i,j]*distance_juzheng[i,j]+ D9 |2 k% ?1 t# f
model.setObjective(objsum,GRB.MINIMIZE)! P6 @' g( e0 \) J3 n
约束条件1 o, a: m3 K8 F+ |3 o1 l3 w1 M' u! s* N
: i5 L7 h8 j) S8 A/ A
#构造约束条件for i in range(0,data_num): constrsum=sum(x[i,:]) model.addConstr(constrsum==1)+ j9 G% n4 G# R7 d3 q
for j in range(0,data_num): constrsum1=sum(x[:,j]) model.addConstr(constrsum1==1)" L$ Z, [9 c9 @; c2 n+ n
for i in range(1,data_num): for j in range(1,data_num): if(i!=j): model.addConstr((u-u[j]+data_num*x[i,j])=data_num-1)
+ R& I( V# P4 i) w5 [4 U$ ~; \优化求解+ z; x; Y1 }& c4 {4 r
model.optimize()8 M5 V+ I" L) J! G3 F
完整代码 8 t; ~ D7 H z, u% h4 v7 _7 m
: r& j0 P0 N$ y6 \+ Q$ l1 u. ^
# 带二次项的规划问题from gurobipy import *import numpy as np( e/ K' T+ Q' n) M- v
model=Model("question1")# x点坐标data_x=[565,25,345,945,845,880,25,525,580,650,1605,1220,1465,1530,845,725, 145,415,510,560,300,520,480,835,975,1215,1320,1250,660,410,420,575,1150,700, 685,685,770,795,720,760,475,95,875,700,555,830,1170,830,605,595,1340,1740]# y点坐标data_y=[575,185,750,685,655,660,230,1000,1175,1130,620,580,200,5,680,370,665, 635,875,365,465,585,415,625,580,245,315,400,180,250,555,665,1160,580,595, 610,610,645,635,650,960,260,920,500,815,485,65,610,625,360,725,245]3 k5 j1 y( o- R! M1 O( q
data_num=len(data_x)
7 M% ]$ i, R9 P( O5 ?distance_juzheng=np.zeros((data_num,data_num))
$ v/ p; ^ y0 y, v3 u6 Y+ Q* }for i in range(0,data_num): for j in range(0,data_num): if (i==j): distance_juzheng[i,j]=100000 else: distance_juzheng[i,j]=np.sqrt(np.square((data_x-data_x[j]))+np.square((data_y-data_y[j])))
0 V1 j' d* w+ H#定义变量x=model.addMVar((data_num,data_num),lb=0,ub=1,vtype=GRB.BINARY) #lb变量下限, ub变量上限 u=model.addMVar((data_num),vtype=GRB.CONTINUOUS) #lb变量下限, ub变量上限
2 {# A9 z; T0 r. B h5 Y- ?" W#构造目标函数objsum=[]for i in range(0,data_num): for j in range(0,data_num): objsum=objsum+x[i,j]*distance_juzheng[i,j]) v$ F+ x# j/ O; o% z8 v
model.setObjective(objsum,GRB.MINIMIZE)( q) C; t7 B' t D
#构造约束条件for i in range(0,data_num): constrsum=sum(x[i,:]) model.addConstr(constrsum==1)& P* x' V0 y3 G3 V" |1 i
for j in range(0,data_num): constrsum1=sum(x[:,j]) model.addConstr(constrsum1==1)" P( M2 Y& _' r$ k. \- Y9 Q* q# `8 p
for i in range(1,data_num): for j in range(1,data_num): if(i!=j): model.addConstr((u-u[j]+data_num*x[i,j])-1)
- ~) n( x2 a, i! G6 {7 b$ }model.optimize()best=(x.X).astype(int)print(f"最优目标值为:{model.ObjVal}")print(f"最优分配为:{best}")/ S: Y$ v" I p) g: G# q
ddbtixqhd3o6408889117.png

0 V% C( R' d3 N* }- v; C% Z z- d B& M Q) c
与MATLAB得到的结果一致
# b/ d" _$ F; P+ h知识点拨:
$ F2 q# }" P5 @! E3 [1 y& o0 q) k4 Z6 O
intlinprog寻找约束非线性多变量函数的最小值
g: o3 F3 ?9 i4 Q' s# z1 f% p) P, c! M- F/ O
语法x = intlinprog(f,intcon,A,b)4 @1 T% _- r# j8 @
x = intlinprog(f,intcon,A,b,Aeq,beq)
0 t4 X& r2 a& N2 E) z3 fx = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)
5 H3 s4 u* Z) X: j: @% S) t; w cx = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub,x0)7 l; u! I/ e. e6 `' @6 Y2 O; v O
x = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub,x0,options)! c, U" f' f A/ m. m, ]! ^. {
x = intlinprog(problem)( K5 @& n& d9 G$ e
[x,fval,exitflag,output] = intlinprog(___)
) H3 {$ v# q) M, x8 z5 e w9 ~( L0 t" |. |: X
说明0 ~# ?8 C& i9 T* F
) J5 d i9 @# Y/ K. Fx = intlinprog(f,intcon,A,b) 最小化 f'*x,使得 intcon 中的 x 分量是整数,且 A*x ≤ b。
& m, I4 ^! I7 @" Z" q2 vx = intlinprog(f,intcon,A,b,Aeq,beq) 求解上述问题,同时还满足等式约束 Aeq*x = beq。如果不存在不等式,请设置 A = [] 和 b = []。
/ ~$ K7 f! I, f1 _& B, b" c示例" U7 }% F: @7 Z0 ^6 i9 {
x = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub) 定义设计变量 x 的一组下界和上界,使解始终在 lb ≤ x ≤ ub 范围内。如果不存在等式,请设置 Aeq = [] 和 beq = []。. H+ J$ d. [3 P- }" J
示例
; b: C( o9 o+ N8 ~5 E9 r% w! n, ux = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub,x0) 使用初始可行点 x0 进行优化。如果不存在边界,请设置 lb = [] 和 ub = []。
' ]# A: C% h" y, C8 r4 P: D
# R. D$ O& P* z: Q% S, g' h( c4 t
5 H `. W; t3 G c5 {【官方intlinprog文档传送】:
& _0 f6 }& }' t2 s" j! e) D7 ~9 f! v8 P8 q5 W
9 }; t& U! C9 Z! R/ W6 W6 F5 Y
1uus4emi02h6408889217.png
 & K$ [2 R* _; R
& K$ [2 R* _; R
$ i! ]7 S: b% w/ Q
扫一扫0 _1 a0 e# v) g+ z" b( Z! ^ g
) t8 p! S. S/ U; c
- \! R. M+ d9 O' }. pEND( P; K( A, r: B. z$ O! O0 N1 a! t
好书推荐:) S: ?3 q4 `% R5 U* P* |
本书共分15章,内容包括数学建模概论,初等模型,微分方程模型,种群生态学模型,线性规划模型,非线性规划模型,层次分析模型,随机模型,动态规划模型,图论模型,最短路模型,网络流模型,数学建模竞赛案例选讲,MATLAB软件使用简介等。( J* z* Y# }+ H
参考资料:9 V" ]% g4 }1 ^6 }: _4 u, z
【1】https://item.jd.com/13422442.html MATLAB智能优化算法:从写代码到算法思想% C8 @ ~: S/ S7 ]- S: y9 x1 R
【2】https://www.jianshu.com/p/e1c45b3d8d8a' E: G5 i M4 V7 z# m" O: j
【3】https://ww2.mathworks.cn/help/optim/ug/intlinprog.html
( X1 b$ _/ } n, w$ {
* E! Z) N- f( j" y. R# T往期精彩回顾2 d+ c. X, t' |2 x" i' b1 J7 d/ U
rgkvtyfoytd6408889317.png

' | q: b. r* J" D& g9 |推荐 | 【建模算法】BP神经网络推荐 | 【建模算法】K-means聚类推荐 | 【建模算法】多层复杂BP神经网络推荐 | 【建模算法】旧金山犯罪事件数据量化分析. t- R) t* m, _- H! P8 h: y/ f
atg1s3omo2y6408889417.png
 8 P' J0 ?% O- G8 o- L' H* n8 n
8 P' J0 ?% O- G8 o- L' H* n8 n
b$ F+ k. K3 N
s1tov3w0gpl6408889517.jpg
 ( T- x8 d( ~- H; l
( T- x8 d( ~- H; l
2 N$ B; g+ l R1 X" q# K
↓↓↓ 点击"阅读原文" 【加入QQ交流群】 |
 /1
/1 