Nature Communications | Floquet拓扑耗散Kerr孤子与非公度频率梳

逍遥设计自动化

引言
6 i1 `; N( C9 d使用具有Kerr非线性的微环谐振器产生相干光频梳，显著推进了对时域耗散孤子及其应用的基础认识。传统的Kerr频率梳的特点是在频率上呈现相位锁定、等距分布的谱线。然而，最新研究发现了一种新型的Floquet拓扑孤子频率梳，这种频率梳出现在利用Floquet拓扑设计的二维强耦合谐振器阵列中[1]。

f1s2txokaw16404961717.png

4 N, h7 A$ m) U, N. n$ XFloquet拓扑孤子系统基础
& P. G% h' h6 w) }3 q/ R- g该系统由二维方形环形谐振器阵列构成，谐振器之间通过近场耦合与最近邻谐振器相连。谐振器间的耦合强度取决于在阵列中的位置，参数化为κa = sin(θA)和κb = sin(θB)。这种排列形成了包含四个谐振器的单元，使阵列可以容纳最多四个能带。
( r4 z2 _% o, n' X6 p7 P

5vlmbdbzayc6404961818.png

图1：(a)产生Floquet拓扑频率梳的二维环形谐振器阵列示意图，(b,c)AF相位中的传输谱和能带结构，(d-f)边缘态和体态的强度分布。
, [3 ~+ T7 n6 o% B/ c$ y# Q
这些能带的拓扑性质由耦合强度κa和κb决定。当谐振器之间的耦合强度与自由光谱范围（FSR）相当时，系统表现出非平凡的拓扑性质。在这种强耦合状态下，系统被视为Floquet系统，因为无法用常规的有效哈密顿量和单模近似来描述。

) Y& m' |9 ]! k8 ~5 D反常Floquet相位中的非公度频率梳
) {+ D- T( E3 h* O, V* e( y在反常Floquet（AF）相位中，边缘态出现在特定归一化频率失谐附近的所有能带隙中。这种相位被称为"反常"，是因为即使所有能带的陈数为零，边缘态仍然存在。
; Q+ U2 w5 q" M. L9 @: l

qozj22xwcpr6404961918.png

图2：(a-c)AF相位中的能带结构和吸收谱，(d)显示相位锁定超级孤子分子的强度分布，(e)显示超级孤子脉冲的时域输出，(f-h)显示非公度性质的输出频率梳谱。

; F' e9 g3 Z( [! n) @- q9 t当在边缘态共振附近泵浦时，阵列边缘形成Floquet超级孤子分子。在这种状态下，边缘上的三个不同环谐振器各自包含一个相位锁定的单孤子，环中相对位置保持不变。

AF相位中的公度频率梳
通过调节耦合参数并保持在AF相位中，可以产生规则间隔的公度频率梳。

nvdx5jmgwso6404962018.png

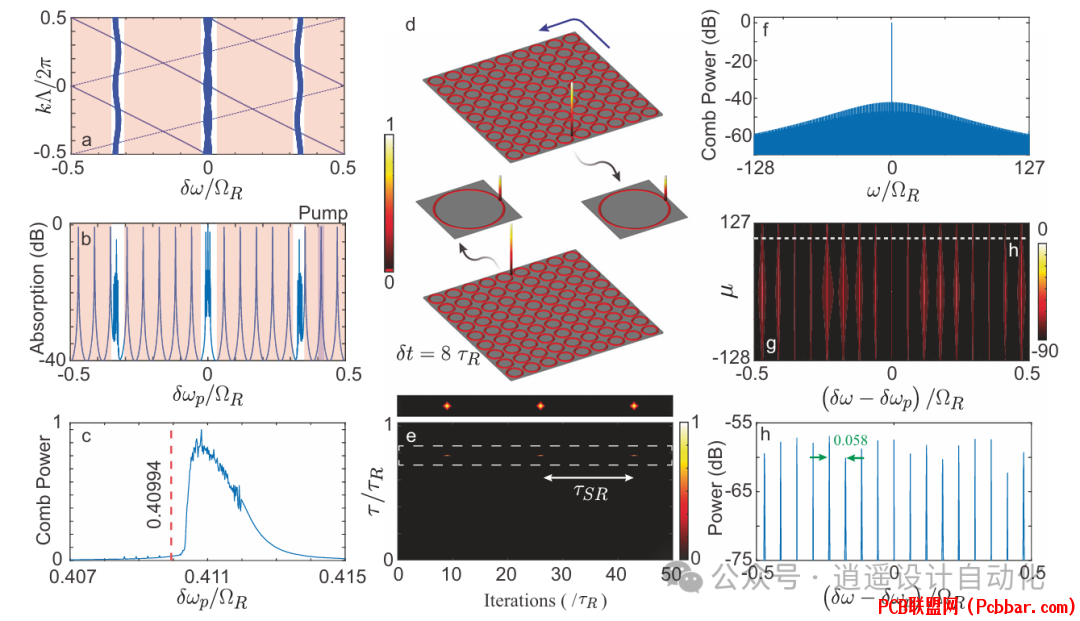
图3：(a,b)显示减小体带宽的能带结构和吸收谱，(c)频率梳功率变化，(d)显示单个超级孤子环绕的强度分布，(e-h)显示规则频率梳产生的时域和频域输出。

当选择耦合参数θA = 0.49π和θB = 0.01π时，该系统仍处于反常Floquet相位，但显著减小了体能带宽度，同时增加了边缘能带宽度。在泵浦频率失谐δωp = 0.40994ΩR时，观察到阵列中形成单个超级孤子。在这种状态下，边缘上只有一个环谐振器包含单个孤子，沿逆时针方向环绕阵列。相应的，时域输出包含单个脉冲，以超环谐振器的往返时间τSR（约17τR）重复。
- e( A4 y4 \  e2 }1 c5 e) u
* X# X' Q" [- D8 [/ A陈绝缘体相位中的孤子分子
陈绝缘体（CI）相位呈现三个体能带，其中两个具有非零陈数，表现出拓扑非平庸性。这三个体能带被两个边缘能带分隔。

cehziwrv14t6404962118.png

6 H- ?9 O7 N6 A, j' D图4：(a,b)CI相位中的能带结构和吸收谱，(c)泵浦功率变化，(d)显示在交替边缘环中形成孤子的强度分布，(e-h)显示单一边缘模式振荡的时域和频域输出。

当在边缘态共振附近调节泵浦频率至δωp = 0.0964ΩR，并调整归一化输入泵浦场至Ein = 0.025时，可以观察到一种全新的孤子分子状态：除了始终存在孤子的角落环外，边缘上的交替环各自精确包含一个孤子。这些孤子在环中的位置保持相位锁定，随时间推移，这种强度分布在阵列中保持稳定。

Floquet频率梳的鲁棒性和可调谐性

c4tox450gk16404962219.png

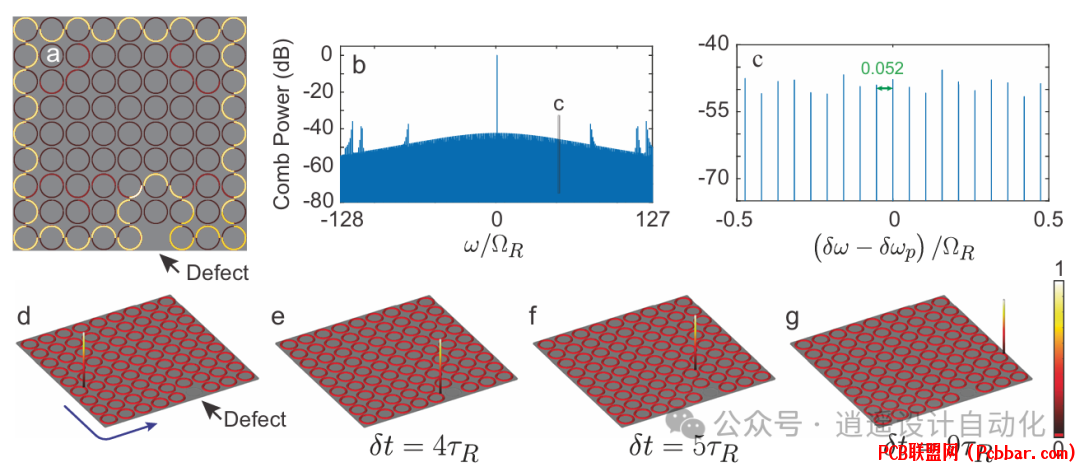
' Y& L8 o  j6 F4 Q4 u图5：(a)边缘态绕过阵列缺陷的路径，(b,c)具有修改线间距的产生频率梳谱，(d-g)展示无相干损失的孤子绕路演示。
9 r% R, J: q& o4 m1 B9 }
) M0 @0 u2 l; B- y, E1 e& j. k# y拓扑边缘态的一个关键特征是对缺陷和无序的鲁棒性。这种特性在强非线性存在的情况下仍然适用于Floquet拓扑孤子。系统可以在标准光子技术平台上实现，如硅氮化物平台，典型参数包括250GHz的FSR、1 MHz的色散以及约8×106的本征品质因数。产生非公度孤子频率梳所需的泵浦功率约为0.6 W，这与典型的Kerr频率梳产生相当。

9 Z  m. |3 f, B% r) k# S5 o总结
% M7 c( [) s6 _  X, Z2 GFloquet拓扑耗散Kerr孤子和非公度频率梳代表了光频率梳领域的重要进展。这种新型频率梳超越了传统频率梳等距频率的定义，为精密测量、光谱学、光通信和光量子技术提供了新的研究方向。这些系统的鲁棒性和可调谐性，加上在存在缺陷时保持相干性的能力，使其在实际应用中具有独特优势。实验参数与现有技术平台兼容，预示着这项技术具有实现的可行性。随着这一领域的持续发展，强耦合非线性谐振器阵列结合Floquet和拓扑设计原理，将在光操控和频率梳产生方面取得更多进展。

参考文献
# g2 a4 W% S4 w# U[1] S. D. Hashemi and S. Mittal, "Floquet topological dissipative Kerr solitons and incommensurate frequency combs," Nature Communications, vol. 15, no. 9642, pp. 1-9, 2024, doi: 10.1038/s41467-024-53995-8.
/ Z) p1 E- Z  O
END

3 B5 ?+ o: |8 s) b0 W* Z9 w
- o+ c3 r& [0 {软件申请我们欢迎化合物/硅基光电子芯片的研究人员和工程师申请体验免费版PIC Studio软件。无论是研究还是商业应用，PIC Studio都可提升您的工作效能。
" i6 c$ \1 l) n# C: n点击左下角"阅读原文"马上申请

欢迎转载

转载请注明出处，请勿修改内容和删除作者信息！



+ p$ p$ Z8 Q( F

skdxfq5tms56404962319.gif

  z! Y" J  \( X* g% D5 U3 {' z. K关注我们
( n0 |  Q" e8 R! h7 s
7 U' s! V$ F! t

( e$ ]$ F' d( w+ G; G lnwxpvz150s6404962419.png " I  E1 t  _# W

4 M' H+ ]' i& ~6 I& D5 A 02f3x1i4krj6404962519.png

4 F3 {% e% n; e6 c/ a1 Z hvj2rlh1av16404962619.png + T6 H( s( s) y" V7 c; X3 {

                     
* A/ w; A9 l7 B


1 v% q1 f* K) \, k2 h/ Q- J关于我们：
5 W5 z. i8 o: n# K  u深圳逍遥科技有限公司（Latitude Design Automation Inc.）是一家专注于半导体芯片设计自动化（EDA）的高科技软件公司。我们自主开发特色工艺芯片设计和仿真软件，提供成熟的设计解决方案如PIC Studio、MEMS Studio和Meta Studio，分别针对光电芯片、微机电系统、超透镜的设计与仿真。我们提供特色工艺的半导体芯片集成电路版图、IP和PDK工程服务，广泛服务于光通讯、光计算、光量子通信和微纳光子器件领域的头部客户。逍遥科技与国内外晶圆代工厂及硅光/MEMS中试线合作，推动特色工艺半导体产业链发展，致力于为客户提供前沿技术与服务。

http://www.latitudeda.com/
（点击上方名片关注我们，发现更多精彩内容）