点击上方蓝字和“好玩的MATLAB”一起快乐玩耍吧!; f# `/ @* \$ f4 q% l5 {* l% B
' e% ?+ p4 E! G8 M9 q4 d0 j/ C, m
ib4ivre4n2w6405197350.jpg
 # S0 s! h2 n4 H, ?
# S0 s! h2 n4 H, ?
好玩的matlab; c, a o: y" Z
带你解锁不一样的matlab新玩法
. t2 G6 H9 \- g t5 v3 O- \
" ?6 w, ]9 e- n# n& K1 V8 S喜欢此推文的小伙伴们记得点赞+关注+分享!" D; ]; Q) O& z( _$ U" X
01, p4 |; C' ]" E1 ]0 O) S5 H4 l
算法用途' U$ D" p L+ J) w2 L% V
) Y. X) G* ]) J7 @; T/ ]9 k5 `
ejnjna1yms46405197450.png

, m2 l/ W! s2 T/ w! {优化算法是指在满足一定条件下,在众多方案中或者参数中最优方案,或者参数值,以使得某个或者多个功能指标达到最优,或使得系统的某些性能指标达到最大值或者最小值。) x1 ^# k4 ~ F& G+ \
多目标规划的概念是 1961年由美国数学家查尔斯和库柏首先提出的。多目标最优化思想,最早是在1896年由法国经济学家V.帕雷托提出来的。他从政治经济学的角度考虑把本质上是不可比较的许多目标化成单个目标的最优化问题,从而涉及了多目标规划问题和多目标的概念。& `, O2 ^, c1 `
+ r* W# |# Q; H K% ~
?* L. p5 H4 Z$ v/ F02; p" N5 Z- N; L2 C" K
实例分析1 A0 Y7 F" ]0 S3 w3 h7 {+ G2 ?9 e
4 q& k! ]/ X9 I d* Y
多目标规划用得比较多的主要有以下几种形式
" m. X- `$ y- T6 B# O( A% c第一种是通过加权的方式将多目标优化转化成单目标优化,不过加权权重比较难确定5 [8 u4 K$ x8 T; W3 e
0 Y J6 k2 o" P
lsjgn2loyaq6405197550.png
 3 H9 r9 S+ P0 s- m1 k
3 H9 r9 S+ P0 s- m1 k
第二种是goal attain 的形式,将原来的多目标转化成新的优化问题,和单个目标的最优化进行比较,目标是与原来单个最优化目标最小
! f7 k- A; e# J% x6 c1 L
q2qw0l4mlay6405197650.png
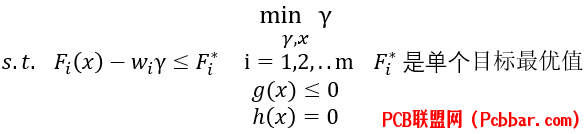
' ^8 O& W; v# N最后就是一些多目标优化的智能优化算法,智能优化算法能在一次运行过程中找到Pareto最优解集中的多个解,且不限于Parato前沿解集的形状和连续性,易于解决不连续的,凹的Pareto前沿。智能优化算法解决多目标优化问题等到下一期出奥
( I; |! e0 i4 H0 j9 t+ u& O! _, @" ?+ p: A( t' V! L
03
3 j( K. U- X' I% J( f$ UMATLAB求解
' [$ T9 l9 x( I/ Y% z5 X! K# a* ~
+ L! I# y% m' l案例一加权方式求解; J: m$ R1 B w. s+ w
/ h& d1 T0 B% m% _5 K
' f1 W# k" O7 J6 L# v( pfmincon是MATLAB的非线性规划求解函数# Q. m, d# l. M/ L( D
[x,fval]=fmincon(fun,x0,A,b,Aeq,Beq,LB,UB,nonlcon)
& a2 ~$ Q, j2 L$ B1 L5 |6 o( r/ Px:求得最优情况下变量的解
- G% g; C% k) c- M& x& Efval:求得最优目标值1 M! H5 Q8 M8 E: H: ]- j6 i
x0:初始解& ?7 U3 m2 C% u
fun:目标函数(符号按最小值标准,若目标是求解机大值可以通过添加负号改成求极小值)
+ d0 C- ~: ?* u* q- ~/ SA:不等式约束的变量系数(符合按小于标准,如果是大于约束可通过加负号变成小于)8 Z& ~" s* m( j' t- a* E$ R6 s0 B2 ?
b:不等式约束的常量' z+ a+ k9 T2 E7 J, e5 V
Aeq:等式约束的变量系数Beq:等式约束的常量LB:变量的下限UB:变量的上限 nonlcon :非线性约束函数表达式
- @* N8 w D, P. X! f9 V: Y* C* R! b5 o! l
优化问题
9 \) y% Y) d; G6 K8 m& I
pffnmefeycx6405197750.png
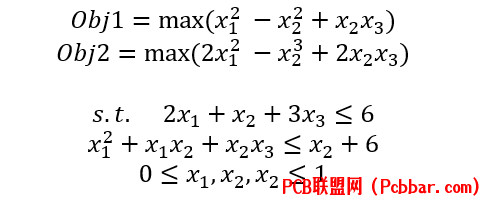 8 e3 x# ?. |3 Z3 J! @
8 e3 x# ?. |3 Z3 J! @
目标函数7 \* U- b* i4 O" u4 p/ m
* Z7 N: D: M F* m8 P+ k
nz4vgzsxo2j6405197850.jpg
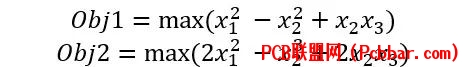
0 E$ q( N; t, e' N0 ^7 S$ T- O5 S5 |$ v- D h8 m: e' d0 w- C
求极大值的问题要转化成极小值,因此加个负号变成求最小值的问题。 通过附权将两种相加,权重可以自定可以根据因变量的范围而定不一定要限制在一定的范围w1=0.5;w2=0.5; %fun = @(x)(-x(1)^2+x(2)^2-x(2)*x(3))*w1+(2*x(1)^2-x(2)^3+2*x(2)*x(3))*w2;
. p' I! \5 [. @* O- x6 Y) O不等式线性约束
; T7 J6 | Q2 a) L1 t% g5 N- J7 f+ H# s8 H6 ?
' I6 m ]! e' b- V6 Y9 L! }
%不等约束A=[2,1,3];%左边特征矩阵b=[6]; %右边) h" u D+ Q) V0 ^" ?
等式线性约束( n1 {/ g5 O! r, a$ m/ ^
- R2 ~0 U; ?) F2 B: Q
无
" F z- X) b& b: G JAeq=[];Beq=[];
* s" v% G4 g2 \变量约束7 {3 Y" {/ w: \, j0 x
5 g+ x% D- v g
8 V. |6 q( C. E& C0 B& p: C+ g m
7 v: z A$ n0 y2 D3 W%变量约束,上限,下限LB=zeros(3,1);UB=ones(3,1);
; z) G* _! D3 g7 E8 E% p非线性约束5 v2 _2 x4 i2 g" ^( c i) O. H
e) \9 ^" H8 k9 m) ^ n+ W8 I! E
" b$ c; s/ ?* o+ Y/ r" F5 p
nonlcon = @unitdisk;function [c,ceq] = unitdisk(x)%c为不等式非线性约束%ceq为等式非线性约束c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;ceq = [];end
% M7 q+ s7 q8 W: h: J- ~9 r全部代码4 d# R( i! C* @" X$ h+ a7 y
clc;clear;close all;%%%初始解,随意给个初始解x0=zeros(3,1);
6 ]2 m% P8 O- H3 d%不等约束A=[2,1,3];%左边特征矩阵b=[6]; %右边
* H( n2 V, G& g F3 N. X* B%等式约束Aeq=[];Beq=[];
) ^! M) M5 K) B L6 O9 f%变量约束,上限,下限LB=zeros(3,1);UB=1*ones(3,1);%优化求解%%w1=0.5;w2=0.5; %fun = @(x)(-x(1)^2+x(2)^2-x(2)*x(3))*w1+(2*x(1)^2-x(2)^3+2*x(2)*x(3))*w2;' Y9 d& m9 R' z* n0 r
nonlcon = @unitdisk;[x1,fval1]=fmincon(fun,x0,A,b,Aeq,Beq,LB,UB,nonlcon);objstr=['目标函数最优值:',num2str(fval1)];disp(objstr)for i=1:length(x1) xstr=['x',num2str(i),'的值为:',num2str(x1(i))]; disp(xstr)end
* x) |. F) ~. U zfunction [c,ceq] = unitdisk(x)%c为不等式非线性约束%ceq为等式非线性约束c=x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6;ceq = [];end
; ?# ~( S5 k8 |; Y8 z" I5 s+ C3 A
zjrnlu20b256405197950.png
 6 W! ?! |- S5 S0 e. d( `& f
6 W! ?! |- S5 S0 e. d( `& f
' L/ y8 C- L1 {7 V
goal attain方式求解1
9 L/ }: r' a0 J B
1 a( D; ?" U S# E* v, a7 o% I5 `+ ]$ ^) i5 c0 g# @* B
+ Q: A% v1 E7 Z2 N
5af5bnu5m2s6405198051.png

7 q" M2 k2 s* d3 S; s优化目标# W* n; @* X h$ K# d1 V% X _
例如有以下两个目标,两个目标的非线性约束有一点差别,其他约束都一样* E K3 N% C$ h, d; g
+ b& e) P3 C8 u/ [7 z6 e
kzg2mfu5g3j6405198151.png
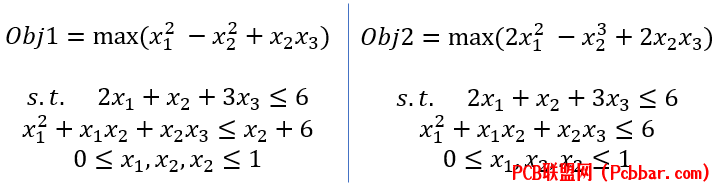 0 m: q4 |# y( f* e+ n/ H
0 m: q4 |# y( f* e+ n/ H
# g8 m0 y/ T* e- w, q
分别得到单个目标最优解做了两次单独的非线性优化,和前面的非线性优化篇方法是一样的,做好初始解,做好线性约束和非线性约束,写好目标带入函数求解即可
5 h$ o/ w% q% z6 [/ D {6 x%初始解,随意给个初始解x0=zeros(3,1);8 q3 t, n! D4 ] ^
%不等约束A=[2,1,3];%左边特征矩阵b=[6]; %右边
! @% n7 ]/ E# y: S7 z5 }7 f. P%等式约束Aeq=[];Beq=[];3 \5 ^% H/ z7 y& e( _& C
%变量约束,上限,下限LB=zeros(3,1);UB=1*ones(3,1);%优化求解%%fun1 = @(x)-x(1)^2+x(2)^2-x(2)*x(3);fun2 = @(x)2*x(1)^2-x(2)^3+2*x(2)*x(3);%%nonlcon = @unitdisk;[x1,fval1]=fmincon(fun1,x0,A,b,Aeq,Beq,LB,UB,nonlcon);objstr=['目标函数最优值:',num2str(fval1)];disp(objstr)for i=1:length(x1) xstr=['x',num2str(i),'的值为:',num2str(x1(i))]; disp(xstr)endnonlcon1 = @unitdisk1;[x2,fval2]=fmincon(fun2,x0,A,b,Aeq,Beq,LB,UB,nonlcon1);objstr=['目标函数最优值:',num2str(fval2)];disp(objstr)for i=1:length(x2) xstr=['x',num2str(i),'的值为:',num2str(x2(i))]; disp(xstr)end
. ]7 ?+ J7 B( L( R2 o6 T% ifunction [c,ceq] = unitdisk(x)%c为不等式非线性约束%ceq为等式非线性约束c=[x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6];ceq = [];endfunction [c,ceq] = unitdisk1(x)%c为不等式非线性约束%ceq为等式非线性约束c=x(1)^2+x(1)*x(2)+x(2)*x(3)-6;ceq = [];end 可以求解得到两个单目标函数的最优分别如下,他们取得单个最优的x值不同,因此两者结合肯定会相互牺牲. V$ w- J0 z, `
; C! x$ l( t0 s) C y# O
目标函数最优值:-1.25. U2 T* g% @4 ?* {( v
x1的值为:1. ?4 ^/ [7 r$ a% d4 r' B( N% d! R
x2的值为:0.5" n# c+ M* x6 W0 p. T4 D' m& K7 w
x3的值为:17 B4 F' S& ~0 N4 C$ d4 N. {8 X1 d
c/ e5 q- ~& Q* M" ]4 A
目标函数最优值:-16 }: V2 C8 X1 l# @6 a- e
x1的值为:0.00056595( x$ ]7 o7 ?) N
x2的值为:11 s+ m2 H; Y0 S r
x3的值为:6.4e-07( O! {9 `+ i2 |
' r/ X- V. K3 a" A0 a. ?
确定两个约束的单个最优, z2 z0 I) l. F& U8 P0 k) H% |
goal=[fval1,fval2]; 2 L2 z2 q( s: P
将两个单目标优化结合
# P% V. H( e' V1 S; B, D 约束条件是两个优化目标均需要满足的,因此可以把所有的约束条件直接融合在一起* Y% K, E/ h+ ]/ o1 a+ o) X5 R
7 C7 {, c+ t7 F' U) u W
015uonvlzsj6405198251.png
 ' S. H8 a2 `/ b7 u/ e4 [
' S. H8 a2 `/ b7 u/ e4 [
$ |- _+ H* b* s8 l+ @' Y) @' c. [; G: `8 b( a4 b3 |9 i
目标函数 两个目标函数都比较简单,可以用数学表达式表达,因此目标函数可以写成以下的形式,将目标函数分号隔开func = @(x)[-x(1)^2+x(2)^2-x(2)*x(3);2*x(1)^2-x(2)^3+2*x(2)*x(3)];不等约束7 X$ b/ u+ p5 ]. t
直接用分号将两个非线性约束结合( |" Y8 h/ L9 u* s; t c
function [c,ceq] = unitdisk3(x)%c为不等式非线性约束%ceq为等式非线性约束c=[x(1)^2+x(1)*x(2)+x(2)*x(3)-6;x(1)^2+x(1)*x(2)+x(2)*x(3)-6];ceq = [];end
1 L( o Z4 L3 m7 @- A+ i* t权重
$ T" D: L! { n4 u9 O7 e# V. _) L离两个分别最优的函数差值的权重,可以用于调节两个优化目标量纲不对等的情况
4 Q( L; v! g# X5 k4 ~$ Lweight=[1,1]; * g' R! p6 K9 J# }. c6 u% I" J" \
完整MATLAB代码
3 ]# \" \: ^9 R3 Wclc;clear;close all;%%%初始解,随意给个初始解x0=zeros(3,1);! d( g7 N! ]7 q1 J
%不等约束A=[2,1,3];%左边特征矩阵b=[6]; %右边
: P5 N8 Q& f4 ?%等式约束Aeq=[];Beq=[];5 `& m: q. v* d( |/ }
%变量约束,上限,下限LB=zeros(3,1);UB=1*ones(3,1);%优化求解%%fun1 = @(x)-x(1)^2+x(2)^2-x(2)*x(3);fun2 = @(x)2*x(1)^2-x(2)^3+2*x(2)*x(3);%%nonlcon = @unitdisk;[x1,fval1]=fmincon(fun1,x0,A,b,Aeq,Beq,LB,UB,nonlcon);objstr=['目标函数最优值:',num2str(fval1)];disp(objstr)for i=1:length(x1) xstr=['x',num2str(i),'的值为:',num2str(x1(i))]; disp(xstr)endnonlcon1 = @unitdisk1;[x2,fval2]=fmincon(fun2,x0,A,b,Aeq,Beq,LB,UB,nonlcon1);objstr=['目标函数最优值:',num2str(fval2)];disp(objstr)for i=1:length(x2) xstr=['x',num2str(i),'的值为:',num2str(x2(i))]; disp(xstr)end%% 多目标规划goal=[fval1,fval2];%%nonlcon3=@unitdisk3;func = @(x)[-x(1)^2+x(2)^2-x(2)*x(3);2*x(1)^2-x(2)^3+2*x(2)*x(3)];weight=[1,1];[x,fival]=fgoalattain(func,x0,goal,weight,A,b,Aeq,Beq,LB,UB,nonlcon3);disp('在两个目标的优化结果为')disp(func(x))for i=1:length(x) xstr=['x',num2str(i),'的值为:',num2str(x(i))]; disp(xstr)end%%function [c,ceq] = unitdisk(x)%c为不等式非线性约束%ceq为等式非线性约束c=[x(1)^2+x(1)*x(2)+x(2)*x(3)-x(2)-6];ceq = [];endfunction [c,ceq] = unitdisk1(x)%c为不等式非线性约束%ceq为等式非线性约束c=x(1)^2+x(1)*x(2)+x(2)*x(3)-6;ceq = [];endfunction [c,ceq] = unitdisk3(x)%c为不等式非线性约束%ceq为等式非线性约束c=[x(1)^2+x(1)*x(2)+x(2)*x(3)-6;x(1)^2+x(1)*x(2)+x(2)*x(3)-6];ceq = [];end: J! c# X* D5 _! N' J. a; M# s
可以得到以下的优化结果:+ X; r4 X( ~/ }9 A
在两个目标的优化结果为
1 e- T! X9 E& i. P7 Q; `9 W9 D( c* | 1.0e-15 *# k# [4 S! b. Y# v% H
8 g* H6 @8 l9 W! O% G -0.2220
% f; F: R' g' H! n" ^ 0.4441( @8 y& T: l8 j) T# b
% o, p4 E, L4 hx1的值为:1.4901e-08 w- y' x% F4 c- f
x2的值为:-3.6734e-40
4 r+ ^6 H8 m" n0 L; ?x3的值为:0' U. K& B9 d5 O2 [# Q
Y$ D/ q5 ~4 _9 [6 D$ F# S. V) G
goal attain方式求解2
8 D* [7 m2 `- s, `5 I" U7 o/ W3 W7 i: y
1 p& f4 c& P& T/ U
优化问题7 Q! p) N" l* {3 K; E
接下来看一个稍微复杂的优化问题,是一个10维的变量,有以下两个目标% J# A9 L* P9 v& ]) c n1 h1 P9 y
/ {8 `* S1 f9 F7 Q( ~9 L# c
h3uzw3isyex6405198351.png

4 h0 h2 P$ ~8 j' y4 s: A5 n目标函数9 a( ~; \- @, o& q5 i4 ~2 i
整体思路和前面差不多,主要是目标函数变复杂了很多,目标函数不好直接用数学表达式写,需要用函数写,因此把目标做成了函数4 q$ t# n0 p/ p% i% B) K G4 |- }/ [
单个目标函数
- I8 f, o9 i: [function y1=obj1(x) [dim, num] = size(x); tmp = zeros(dim,num); tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2; tmp1 = sum(tmp(3:2:dim,:)); % odd index tmp2 = sum(tmp(2:2:dim,:)); % even index y1 = x(1,:) + 2.0*tmp1/size(3:2:dim,2);% y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);endfunction y2=obj2(x) [dim, num] = size(x); tmp = zeros(dim,num); tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2; tmp1 = sum(tmp(3:2:dim,:)); % odd index tmp2 = sum(tmp(2:2:dim,:)); % even index% y2 = x(1,:) + 2.0*tmp1/size(3:2:dim,2); y2 = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);end
# ?) e. M2 u. K: d, R: p' }整合两个目标函数
* m3 h% ]% X% L' m$ y/ J将两个目标函数写在一起,分行写function y=obj3(x) [dim, num] = size(x); tmp = zeros(dim,num); tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2; tmp1 = sum(tmp(3:2:dim,:)); % odd index tmp2 = sum(tmp(2:2:dim,:)); % even index y(1,:) = x(1,:) + 2.0*tmp1/size(3:2:dim,2); y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);end1 P; a t) ?8 i: ^1 F
约束条件基本没什么,设置为空就行
8 ^4 ~0 u/ k( O) d" C2 R% v! `. M/ X) l
全部求解代码
$ v% a! n( q% ~- p3 n F* L- r" m" {4 B1 V( X" G, ]: e! v
%% 非线性规划1clc;clear;close all;%%%初始解,随意给个初始解x0=zeros(10,1);%%%不等约束A=[];%左边特征矩阵b=[]; %右边%等式约束Aeq=[];Beq=[];%%%变量约束,上限,下限LB=-1*ones(10,1);LB(1)=0;UB=1*ones(10,1);%优化求解%%fun1 = @obj1;fun2 = @obj2;%%nonlcon = [];[x1,fval1]=fmincon(fun1,x0,A,b,Aeq,Beq,LB,UB,nonlcon);objstr=['目标函数最优值:',num2str(fval1)];disp(objstr)for i=1:length(x1) xstr=['x',num2str(i),'的值为:',num2str(x1(i))]; disp(xstr)end[x2,fval2]=fmincon(fun2,x0,A,b,Aeq,Beq,LB,UB,nonlcon);objstr=['目标函数最优值:',num2str(fval2)];disp(objstr)for i=1:length(x2) xstr=['x',num2str(i),'的值为:',num2str(x2(i))]; disp(xstr)end%% 多目标规划goal=[fval1,fval2];func = @obj3;weight=[1,1];[x,fival]=fgoalattain(func,x0,goal,weight,A,b,Aeq,Beq,LB,UB,nonlcon);disp('在两个目标的优化结果为')disp(func(x))for i=1:length(x) xstr=['x',num2str(i),'的值为:',num2str(x(i))]; disp(xstr)end%%function y1=obj1(x) [dim, num] = size(x); tmp = zeros(dim,num); tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2; tmp1 = sum(tmp(3:2:dim,:)); % odd index tmp2 = sum(tmp(2:2:dim,:)); % even index y1 = x(1,:) + 2.0*tmp1/size(3:2:dim,2);% y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);endfunction y2=obj2(x) [dim, num] = size(x); tmp = zeros(dim,num); tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2; tmp1 = sum(tmp(3:2:dim,:)); % odd index tmp2 = sum(tmp(2:2:dim,:)); % even index% y2 = x(1,:) + 2.0*tmp1/size(3:2:dim,2); y2 = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);endfunction y=obj3(x) [dim, num] = size(x); tmp = zeros(dim,num); tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2; tmp1 = sum(tmp(3:2:dim,:)); % odd index tmp2 = sum(tmp(2:2:dim,:)); % even index y(1,:) = x(1,:) + 2.0*tmp1/size(3:2:dim,2); y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);end3 H$ p( A9 G5 T% o- Y: G: d
E+ ~6 x3 m) }1 h4 b3 W2 U求解得到结果如下所示:
( y5 C6 `- S4 D5 ]: [在两个目标的优化结果为
4 o( }/ x( E( v, {6 v8 n- g/ I+ G 0.38372 Z P9 l' T) F# f r% h
0.5008( O: s5 v# o- k$ d% K3 `
( r0 f3 e5 k% ^- E9 C
x1的值为:0.3773% g+ e' F$ S' F7 L
x2的值为:1
v! E) M2 R4 Gx3的值为:1
$ h5 e4 j, S/ A; I' i; q4 \) fx4的值为:0.459337 [2 [7 E, [7 ]
x5的值为:0.72692) d( @( M/ c. ]4 |, }6 S1 M3 c3 D
x6的值为:0.414776 h" q& \! P9 E
x7的值为:0.13379
( I' q% O @2 z3 i6 m8 d& C: Xx8的值为:0.098991
4 w! E5 |! t$ p9 J1 x9 q5 xx9的值为:-0.58879% [' Q8 g4 k& a3 ^6 ]( M5 }) Y
x10的值为:-0.909343 I9 ~/ j1 P: |
5 ^9 V1 Q8 Q& U
参考资料:- g. I9 g4 v% I- P/ n8 s4 V$ q
【1】https://item.jd.com/13422442.html MATLAB智能优化算法:从写代码到算法思想2 b; k: \ p8 @* d4 }% D
【2】https://ww2.mathworks.cn/help/optim/ug/intlinprog.html; @% o& c* n/ C/ u S
往期精彩回顾) J% F) k& s) F; c7 _% W7 q) ~
ihyzhcjvttl6405198451.png

" [) z. Q# ]) J推荐 | 【建模算法】BP神经网络推荐 | 【建模算法】K-means聚类推荐 | 【建模算法】多层复杂BP神经网络推荐 | MATLAB|聚类散点图|边际图|核密度填充图
$ i. ^0 a. `/ g7 y) _' ^
bwqrk00qgox6405198551.png

+ i: f8 s# a0 S' p* h
Y: c- W6 A/ n7 p0 u
an3fpiepk5h6405198651.jpg

|